When discussing slopes, understanding what a 30% slope means can be crucial for various applications, from construction to outdoor activities.
A 30% slope indicates that for every 100 horizontal units, the elevation changes by 30 units. This steepness is significant, especially for tasks such as grading land or evaluating hiking trails.
The concept of slope is often expressed as a percentage, which captures the relationship between the vertical rise and the horizontal run.
To convert a slope percentage to degrees, one can use the tangent function, which provides a clearer perspective on how steep a slope truly is. For a 30% slope, the angle is approximately 16.7 degrees, making it an important figure for planners and builders who need to assess usability and safety.
In outdoor scenarios, including sports and recreation, the degree of a slope can affect everything from trail design to the practice of skiing in mountainous regions. Recognizing how a 30% slope impacts these environments can help in making informed decisions about usage, safety, and construction.
Understanding Slope Percentages

Slope percentages are essential in various fields, including construction, hiking, and engineering. They provide a clear way to understand the steepness or incline of a surface.
This section explains the definitions, calculation methods, and differences between slope percentage and degrees.
Defining Slope and Its Measurements
The slope is defined as the ratio of vertical change to horizontal change, often known as “rise over run.” The rise refers to the vertical distance gained, while the run is the horizontal distance covered.
Slope can be expressed as a percentage, which is calculated by taking the rise, dividing it by the run, and then multiplying by 100.
For instance, if a hill rises 3 feet over a horizontal distance of 36 feet, the slope percentage would be (3/36) x 100 = 8.3%. This method measures how steep the incline is.
Slope Calculation Methods
There are several methods to calculate slope percentage.
The most straightforward method uses the formula:
[ \text{Slope Percentage} = \left( \frac{\text{Rise}}{\text{Run}} \right) \times 100 ]
Alternatively, using trigonometry, one can apply the tangent function.
If the slope angle (in degrees) is known, the rise and run can also be determined using:
[ \text{Slope} = \tan(\text{Angle}) \times 100 ]
To convert the slope percentage back to degrees, the inverse tangent function (arctan) is applied:
[ \text{Angle} = \text{atan}\left(\frac{\text{Slope}}{100}\right) ]
These calculations often rely on tools like a slope percentage calculator for ease and accuracy.
Differences Between Slope Percentage and Degrees
Understanding the difference between slope percentage and degrees is crucial. While both describe the steepness of an incline, they use different formats.
Slope percentage is based on a ratio of the rise compared to the run, expressed as a percentage.
In contrast, degrees provide a direct angle measurement from the horizontal. For instance, a 30% slope translates approximately to a 16.7-degree angle. Recognizing these differences helps in selecting the appropriate measurement for specific applications, whether in construction or outdoor activities.
Knowing both metrics allows for a clearer understanding of how steep a hill or slope may feel during an activity.
Slope Application in Design and Engineering
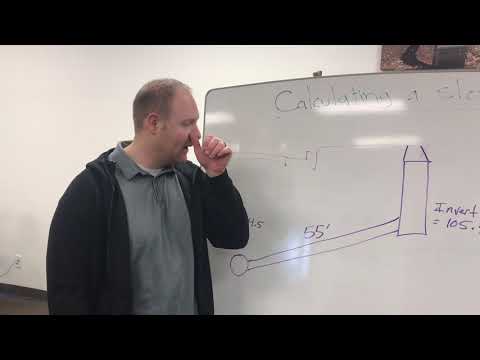
Slope is an essential consideration in various fields like architecture, civil engineering, and infrastructure development. This section discusses how slope influences building designs, infrastructure planning, and accessibility, providing insights on practical applications and regulatory standards.
Slope in Architecture and Civil Engineering
In architecture, slope plays a crucial role in roof design, where a well-planned roof slope enhances drainage and prevents water accumulation. Typical roof slopes range from 2% to 40%, depending on the materials used. Architects must consider the slope gradient for aesthetics and functionality, ensuring that structures can withstand weather conditions.
In civil engineering, slope influences site grading and land development.
A gentle slope, generally less than 5%, is ideal for construction, while steeper slopes present challenges such as erosion and stability issues. The minimum slope for proper drainage is often set at 2%, helping to manage water runoff effectively. Understanding slope ratios aids engineers in designing safe and functional landscapes.
Slope Considerations in Infrastructure
Slope is a key factor in designing effective infrastructure systems. For paved surfaces like roads and sidewalks, a well-calculated slope ratio ensures proper drainage and safety for vehicles and pedestrians. Roads typically have a slope gradient ranging from 1% to 6% to facilitate adequate water runoff.
In utilities such as drainage pipes, proper pipe slope is vital for effective waste flow.
The recommended slope for drainage pipes often varies from 1% to 2%, ensuring that wastewater moves efficiently without risk of blockage. Engineers must adhere to plumbing codes that specify these slopes, maintaining system integrity and functionality.
Accessibility and Regulatory Compliance
Accessibility is critical in slope design, especially on ramps and paths.
The Americans with Disabilities Act (ADA) requires that the maximum slope for wheelchair ramps not exceed 1:12 (approximately 8.33%). This standard ensures that all users can navigate spaces safely.
Other slope considerations involve maintaining accessible routes across various terrains.
Landscape architects must design gradients that comply with regulatory requirements, providing safe and usable public spaces.
Common slopes in architecture often reflect local terrain and physical geography, guiding the design process to create environments suitable for everyone while adhering to accessibility guidelines.

